Alternate Interior Angles Theorem


The alternate interior angles theorem states that if a transversal intersects or cuts two lines that are parallel, then the alternate interior angles are congruent or equal.

In the figure below, the red line is the transversal or the line that cuts or intersects the two blue lines that are parallel. Therefore, the alternate interior angles shown in green, named 1 and 2, are congruent or equal.

Alternate interior angles theorem

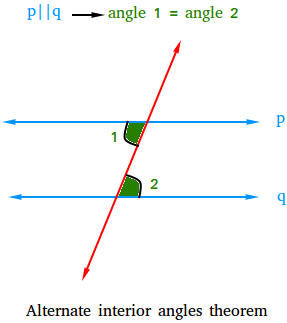
Examples showing how to use the alternate interior angles theorem


1.

Use the figure below to find the measure of angle x.

Alternate interior angles theorem example

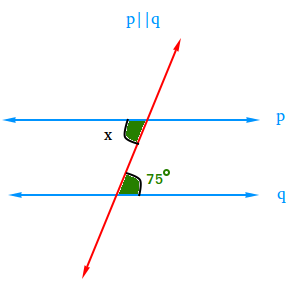
Since line p is parallel to line q, angle x has the same value as the angle whose value is 75 degrees.

x = 75 degrees.

2.

Use the figure below to find the value of a.

Alternate interior angles theorem example

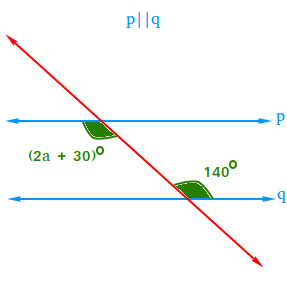
Since line p is parallel to line q, (2a + 30)0 has the same value as the angle whose value is 145 degrees.

2a + 30 = 140

2a + 30 - 30 = 140 - 30

2a = 110

a = 55

Homepage

Math words beginning with the letter a

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: