Common difference of an arithmetic sequence


The common difference of an arithmetic sequence is the fixed number that is added to each number in the sequence, except the first number or starting number. The figure below shows the common ratio for the arithmetic sequence 2, 6, 18, 54, ...

Common difference

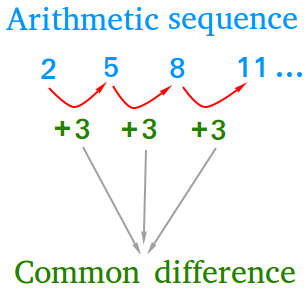
Notice that  5 - 2 = 3, 8 - 5 = 3, and 11 - 8 = 3. The name common difference came from the fact that the difference between consecutive numbers is constant.

Other examples showing what the common difference of an arithmetic sequence is


a.

Arithmetic sequence: 7, 11, 15, 19, ...

The common difference is 4

b.

Arithmetic sequence: 5, 11, 17, 23, ...

The common difference is 6

c.

Arithmetic sequence: 8, 8 + d, 8 + 2d, 8 + 3d, ...

The common difference is d for the following reason:

8 + d - 8 = d

8 + 2d - (8 + d) = 8 + 2d - 8 - d = d

8 + 3d - (8 + 2d) = 8 + 3d - 8 - 2d = d

There is something interesting about c.!

The second number is 8 + d = 8 + 1d 

The third number is 8 + 2d

The fourth number is 8 + 3d 

What can we conclude about the nth number?

Notice that the number in blue is always one less than the term number shown in red. For example, for 8 + 3d, the number in blue is 3 for the 4th number.

We can also say that for 8 + (n - 1)d, the number in blue is n - 1 for the nth.

Therefore, nth term  =  8 + (n - 1)d for the arithmetic sequence 8, 8 + d, 8 + 2d, 8 + 3d, ...

Homepage

Math words beginning with the letter c

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: