What is domain of a rational expression? Definition and examples

The domain of a rational expression is the set of all real numbers for which the rational expression is defined.

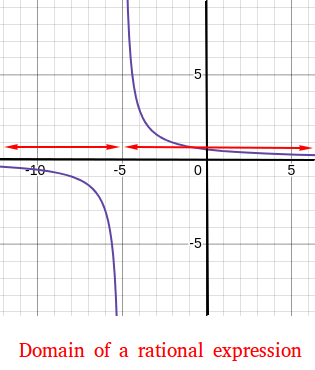Graph and domain of 3 / (x + 5)

How to find the domain of a rational expression

For example, what is the domain of 3 / (x + 5)? The denominator is x + 5.

To find which number makes the denominator equal to zero, make x + 5 equal to zero and then solve for x.

x + 5 = 0

Subtract 5 from both sides of the equation

x + 5 - 5 = 0 - 5

x + 0 = -5

x = -5

Since x + 5 is equal to zero when x = -5, the domain of 3 / (x + 5) is the set of all real numbers except -5. The domain of 3 / (x + 5) is shown in the graph above with two red lines. We use a small green circle to show that -5 is not included in the domain.

Notice that a number in the domain of 3 / (x + 5) could be equal to something as close to -5 as -5.0001 or -4.9998. 

As long as it is not equal to -5, you are free to pick any number!

How to describe the domain of a rational expression using set-builder notation and interval notation

1.

Set-builder notation

Using the set-builder notation to write the domain of 3 / (x + 5 ), we can write "The set of all real numbers x such that x is not equal to -5" as

{x | x is a real number and x ≠ - 5} or simply {x | x ≠ - 5}.

2.

Interval notation

Using the interval notation to write the domain of 3 / (x + 5 ).

We can write (-∞, -5) ∪ (-5, ∞)

Learn more about interval notation.

More examples showing how to find the domain of a rational expression

Example #1

What is the domain of (x - 2) / 9 ? 

Which number makes the denominator equal to zero?

The denominator is 9 and 9 will never be zero. Therefore, there are no numbers that will make the denominators equal to 0.

The domain of (x - 2) / 9  is all real numbers. 

Example #2

What is the domain of (x² - 5) / (x + 3)(x - 6) ? 

The denominator is (x + 3)(x - 6) and it is equal to zero if (x + 3)(x - 6)  = 0

The factor x + 3 is equal to 0 when x = -3 and the factor x - 6 = 0 when x = 6.

The domain of (x² - 5) / (x + 3)(x - 6) is the set of all real numbers except -3 and 6.

Using the set-builder notation to write the domain of (x² - 5) / (x + 3)(x - 6), we can write the following:

{x | x is a real number and x ≠ - 3 and x ≠ 6} or simply {x | x ≠ - 3 and x ≠ 6}.

Using the interval notation to write the domain of (x² - 5) / (x + 3)(x - 6), we can write the following:

 (-∞, -3) ∪ (-3, 6) ∪ (6, ∞)