Length of a circular arc


The length of a circular arc, also called arc length , can be defined as a fraction of a circle's circumference.  

The distance around an entire circle is called the perimeter of the circle or circumference. However, the distance around a portion of a circle is called arc length. 

The measure of an arc is not the same as the arc length since the measure of an arc is expressed in degrees while the arc length is expressed is inches, meters, etc.

How to find the length of a circular arc


The length of a circular arc is the product of the ratio (measure of the arc / 360) and the circumference of the circle (2πr)

Length of a circular arc

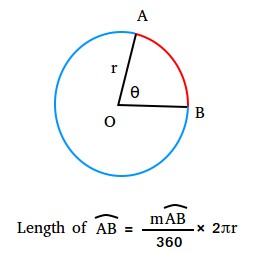
Notice that the measure of an arc AB equals the measure of the central angle θ with rays intercepting the arc's endpoints.

Suppose θ is equal to 360 degrees, then the measure of arc AB is 360.

Length of arc AB = (360/360) × 2πr

Length of arc AB = 1 × 2πr = 2πr

Since 360 degrees is a full circle, it makes sense that 2πr is length of the full circle.

The formula above shows that if θ is a degree measure, then the  length of arc AB = (θ/360) × 2πr

If θ is a radian measure, then the measure of the central angle is 

(θ/2π radians) or simply θ/2π 

Length of arc AB = (θ/2π) × 2πr

Length of arc AB = (θ/2π) × 2πr/1

Length of arc AB = (θ × 2πr)/(2π × 1)

Length of arc AB = (θ × 2πr)/2π

Length of arc AB = (θ × r)

Let r be the radius of a circle, and let θ be radian measure of the central angle of the circle. 

If s is the length of a circular arc intercepted by the central angle, then s = rθ

Therefore, the length of a circular arc can also be defined as the product of the radius of the circle and the radian measure of the central angle of the circle. 

Example showing how to find the arc length

A circle has a radius of 20 inches. Find the length of the arc intercepted by a central angle of π/4.

s = rθ = 20 × π/4 = 5π = 5(3.14) = 15.7 inches

You could also convert π/4 into degrees if you wish, but then you have to use the formula below.

Length of arc AB = (m arc AB / 360) × 2πr

π/4(180/π) = 180/4 = 45

Length of arc AB = (45/360) × 2πr

Length of arc AB = (0.125) × 2π(20) 

Length of arc AB = (0.125) × 40π = 5(π) = 15.7 inches

Homepage

Math words beginning with the letter a

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: