What is the Slope of a Line? Definition and Examples


What is the slope of a line? The slope of a line is the ratio of the rise to the run between any two points (x1, y1) and (x2, y2).

The rise is the distance straight up (or vertical distance) between the two points and the run is the horizontal distance between the two points. 

Slope of a line

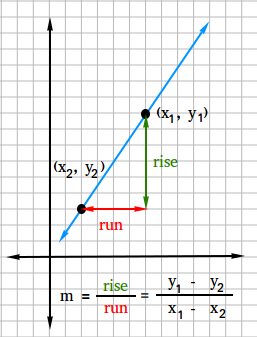
The rise can also be called vertical change and the run can also be called horizontal change.

Different ways to define the slope of a line


Slope  = vertical change / horizontal change

Slope  = vertical distance / horizontal distance

Slope = rise / run

Slope = (y1 - y2) / (x1 - x2)

Example showing how to find the slope of a line


Use the two points shown in black in the figure above to find the slope of the line.

Slope  = rise / run = 6 / 4 = 3 / 2

Slope = (y1 - y2) / (x1 - x2)

(x1, y1) = (6, 9) and (x2, y2) = (2, 3)

Slope = (y1 - y2) / (x1 - x2)

Slope = (9 - 3) / (6 - 2)

Slope = (6) / (4) = 3 / 2

Homepage

Math words beginning withe the letter s

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: