What are Vertical Angles? Definition and Examples

Vertical angles are angles that are on the opposite sides of two lines that intersect. In the figure below, angle a and angle b are vertical angles.

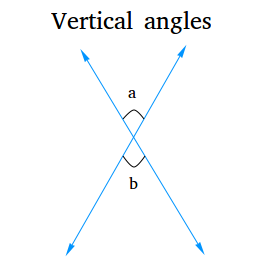
Are vertical angles congruent?

Yes, vertical angles are congruent or equal. For example, referring to the figure above, if angle a is equal to 70 degrees, angle b is also equal to 70 degrees. Why are vertical angles congruent? Check vertical angles theorem to see a proof!

Can vertical angles be adjacent?

No, this is impossible! Vertical angles are opposite to each other, never adjacent or next to each other.

Can vertical angles be complementary?

Yes, it is possible for vertical angles to be complementary. Complementary angles add up to 90 degrees. 

Referring to the figure above, this means that angle a  + angle b = 90 degrees.

Since angle a = angle b, we get angle a + angle a = 90 degrees.

2 angle a = 90 degrees

angle a = 45 degrees.

angle b = 45 degrees.

Vertical angles are complementary when each of the two angles is equal to 45 degrees.

Can vertical angles be supplementary?

Yes, it is possible for vertical angles to be supplementary. Supplementary angles add up to 180 degrees. 

Referring to the figure above, this means that angle a  + angle b = 180 degrees.

Since angle a = angle b, we get angle a + angle a = 180 degrees.

2 angle a = 180 degrees

angle a = 90 degrees.

angle b = 90 degrees.

Vertical angles are supplementary when each of the two angles is equal to 90 degrees.

Vertical angles in real life

• Railroad crossing sign

• Putting one index finger on top of another index finder.

• Legs of an iron stand