What is a bar graph ?


A bar graph is a kind of graph that we use to compare quantities. Rectangular bars are used to compare these quantities and we can arrange these bars either vertically or horizontally.

The vertical bar graph below shows people's favorite seasons of the year.

Vertical bar graph

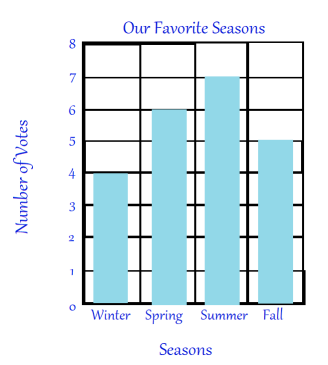
1. What is the least favorite season according to the bar graph?

The least favorite season is Winter.

2. What is the most favorite season according to the bar graph?

The most favorite season is summer.

3. About how many people like summer more than winter?

Seven people said they preferred summer and four people said they preferred summer. Therefore, three more people preferred summer than winter. 

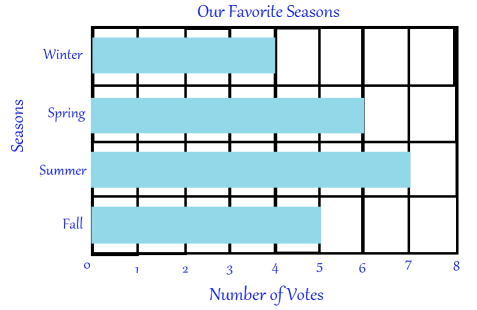
We can also arrange the information with a horizontal bar graph.

Horizontal bar graph

Home

Math words beginning with the letter b

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: