What is a Zero Pair? Definition and Examples of Zero Pairs

What is a zero pair in math? A zero pair is created when you add 1 and -1 and the sum is zero.

Suppose 1 green circle represent +1 and 1 orange circle represent -1.

Then, a pair of circles made of 1 green circle and 1 orange circle is a zero pair.

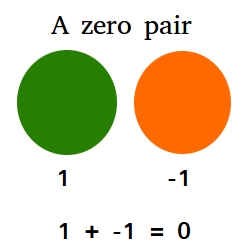
What are Zero Pairs?

If you put 5 green circles and 5 orange circles next to each other, then you have 5 zero pairs. This is the same as adding 5 and -5 to get zero.

If you put 12 green circles and 12 orange circles next to each other, then you have 12 zero pairs. This is the same as adding 12 and -12 to get zero.

If you put 500 green circles and 500 orange circles next to each other, then you have 500 zero pairs. This is the same as adding 500 and -500 to get zero.

More Zero Pair examples

Here are a few more examples of zero pairs

• {5, -5}
• {-18, 18}
• {-100, 100}
• (1200, -1200}
• {69, -69}

How Can You Use Zero Pairs to Solve Problems?

Zero pairs can help you add integers quickly in many cases.

For example, if you are adding 500 and -522, you just need to recognize that 500 and -500 are zero pairs to quickly get an answer.

500 + -522 = 500 + -500 + -22 = 0 + -22 = -22

More examples

Add -85 and 96

-85 + 96 = -85 + 85 + 11 = 0 + 11 = 11

Add 656 and -690

656 + -690 = 656 + -656 + -34 = 0 + -34 = -34