What is an Odd Function? Definition and Examples


What is an odd function? A function f is an odd function if f(-x) = -f(x) for all x in the domain of f. 

For example f(x) = x3 is an odd function

f(-2) = (-2)3 = -2 × -2 × -2 = -8 and f(2) = (2)3 =  2 × 2 × 2 = 8

f(-2) = -8 = -f(2)

f(-1) = (-1)3 = -1 × -1 × -1 = -1 and f(1) = (1)3 =  1 × 1 × 1 = 1

f(-1) = -1 = -f(1)

In general, let x represent any number in the domain of f.

Then, f(-x) = (-x)3 = -x × -x × -x = -x × x2 = -x3 and f(x) = x3

f(-x) = -x3 = -f(x) 

For f(2) = 8 and f(-2) = -8, the points are (2, 8) and (-2, -8)

For f(1) = 1 and f(-1) = -1, the points are (1, 1) and (-1, -1)

Notice that f(0) = 03 = 0, so there is a single point (0,0)

Now, try to graph these five points on a coordinate system.

(2, 8), (-2, -8), (1, 1), (-1, -1), and (0, 0)

Odd function

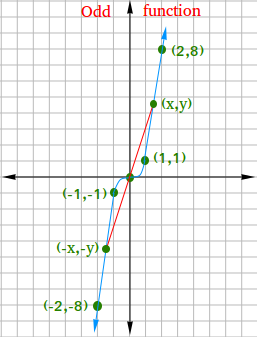
From the graph above, we can make the following two important observations:

  • If a point (-x,-y) is on the graph, the point (x,y) is also on the graph. 
  • The function is symmetric with respect to the origin.

More examples of odd functions

  • f(x) = x3 - 8x
  • f(x) = x5 
  • f(x) = sin(x)
  • f(x) = x7


f(x) = x3 + 1 is not an odd function.

f(-x) = -x3 + 1

f(-x) = -(x3 - 1) 

Since x3 - 1 ≠ x3 + 1, f(-x) ≠ -f(x)

≠

Homepage

Math words beginning with the letter o

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Share this page: